原名: Mutant: Balancing Storage Cost and Latency in LSM-Tree Data Stores
文章目标: 提供一种无感的 cost-performance trade off 的LSM tree实现,将热数据存在fast storage,冷数据存在cold storage
效果一图以言之:
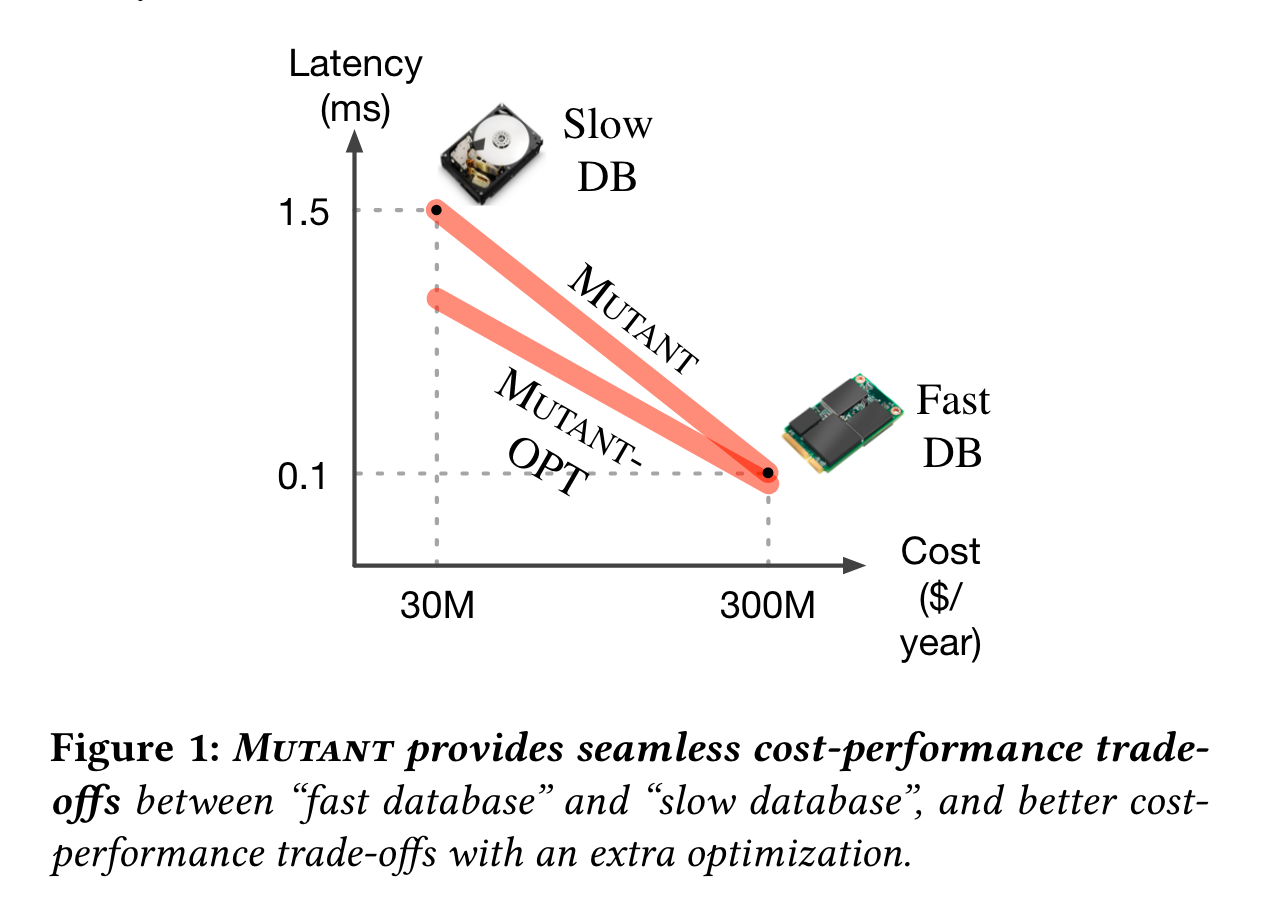
读完感觉没有太多亮点,不过还是记个笔记。
Backgroud·
作者说由于workload的access pattern, LSM中的sstable及sstable的component具有不同的访问频率。
SST文件的locality证明·
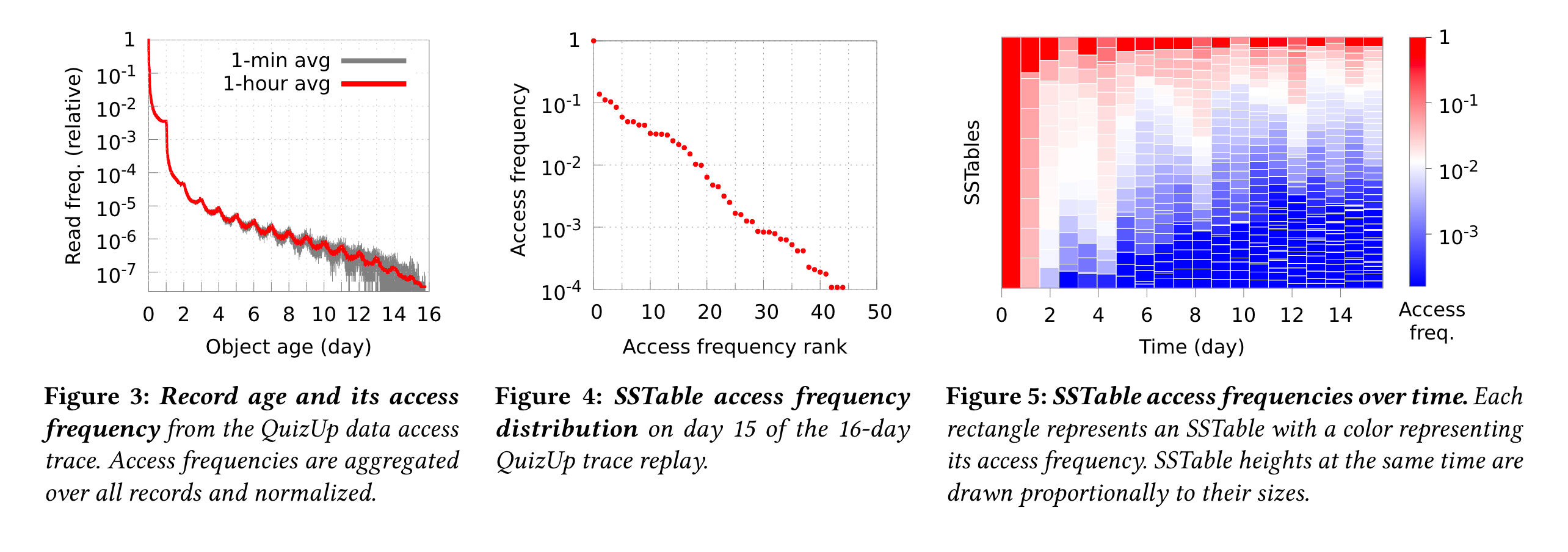
作者用了16天的QuizeUP数据来证明,图3是real world中,随着时间的推进,数据的访问频度。图4证明了不同的sstable的访问频率区别,最热与最冷之间的访问频率差了4个数量级(笔者注:access frequency rank论文中也没解释具体含义,个人关注的是冷数据和热数据的数量分布)。图5证明冷热属性是持久的(笔者注:这个图我是觉得没那么好理解。。。)
SST component locality证明·
不仅SST文件具有热冷属性,SST内部的组件也有热冷区别,SST由metadata和data组成,metadata由bloomfilter和index组成。

明显data、index filter之间的访问频率差别很大。所以如果将所有数据都存在更贵的ssd上是一种浪费,但把所有数据存在廉价的硬盘上性能又无法接受。
System Design·
作者设计了MUTANT,将不同SST分层处理。云产商用户的一个经典SLO(Service Level Objective)是: “we will pay no more than $0.03/GB/month for the database storage, while keeping the storage latency to a minimum”
顺便一提,作者的计价参考价格为:
![image-20241027194548364]()
优化目标建模·
作者将上述目标分为两部分:
- 最小化延迟。 作者认为业界云产商都不敢保证延迟。所以该目标被转化为尽可能将更多访问得多的文件放在fast device(笔者注:有点偷换概念了)
- 保持存储架构 $3/GB/month (3刀? 上文又是说0.03刀,笔误?还是放宽了设计目标?)
最终问题被抽象为:
找到一组sstable子集来存放到fast storage上,保证这堆fast storage的sstable的访问频率sum是最大的,限制在fast storage的容量下。
首先,将成本预算限制转换为存储size的限制,这包含两部分:
- 总的sstable size被分为fast storage和slow storage 两部分
- fast storage和slow storage成本相加不能超过total storage cost
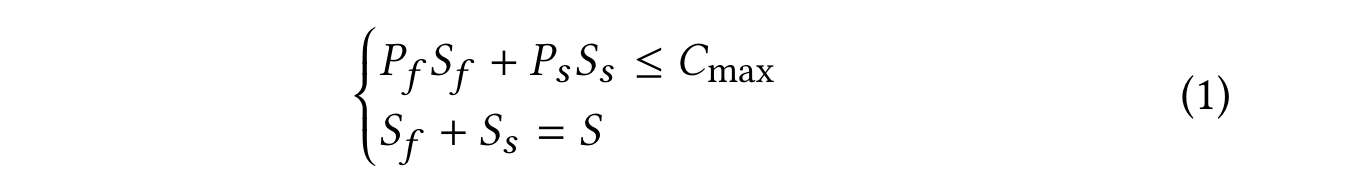
P: 介质的单价成本
S: 介质的size
Cmax: 总成本
将Ss = S -Sf 代换到第一个不等式,可转化为: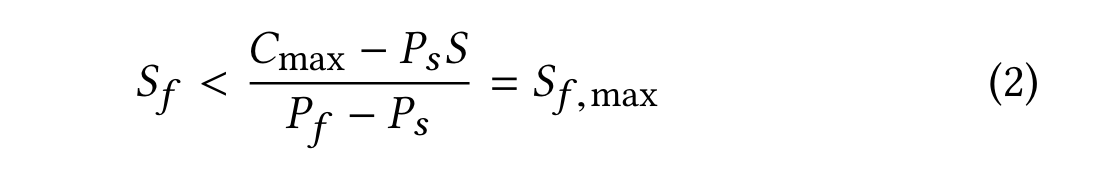
最终优化目标公式为:
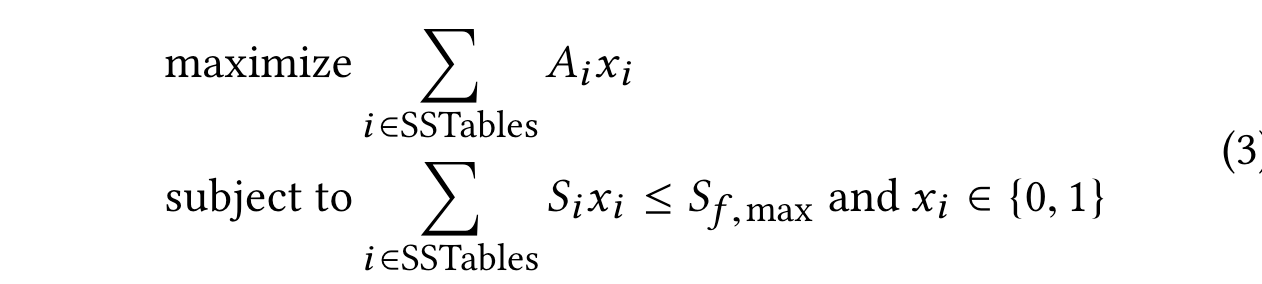
Ai代表每个SSTable的访问频率,Xi等于0或者1,0代表slow,1代表fast。 所以优化目标为最大化访问频率,受限于所有文件的size。上述公式其实就是0 1背包问题。
难得工程上见到经典算法使用场景。
贪心算法模型优化·
背包问题是典型的NP-hard问题,作者用了贪心算法解背包,优先选择价值密度最高的sstable,直到选择不下为止。这里的价值密度定义为: sstable size / access frequence。
用贪心算法解背包问题,最差的场景下,贪心算法解出来的结果比最优算法(动态规划)差2倍。对于文章的场景,那就是延迟会高两倍。
SSTable 热度问题·
考虑到以下两个问题:
- sstable size是变化的,一方面来自配置(如rocksdb为64M,cassandra为160M), compaciont也会带来不同size的sstable
- sstable的热度也是波动的,比如burst写,上游网络中断等。
所以为了平滑热度,作者加了指数平均(笔者注:应该是加权平均?)
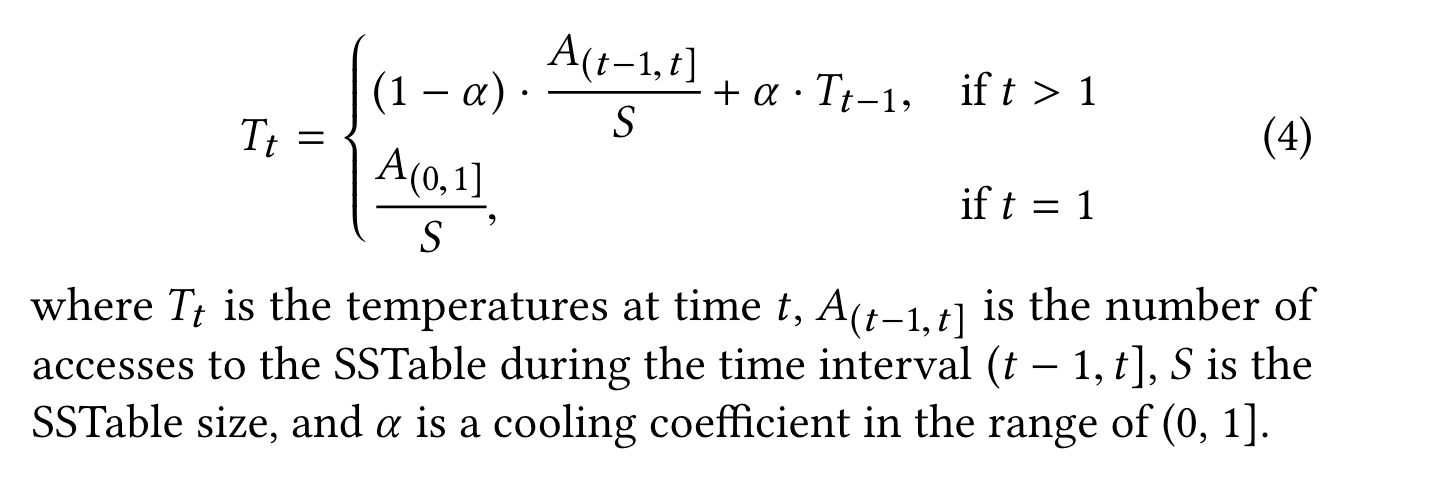
当前SSTable的热度等于当前时间窗口的热度(频率除以size) + 上一个热度的衰减。
阿尔法为衰减协调因子。
SSTable Component优化·
一句话:把所有metadata缓存在内存
Implemention·
实现只用了658行c++代码。
三个API:
- 初始化, 传入不同device的配置,单价等
- 注册monitor,开启access监听
- sstable organization,数据迁移实现。

笔者注:看到这里,个人比较关心的写放大有多少,毕竟设计到数据迁移。 另外比较好奇的是,这些热度信息是怎么持久化的?还有一个问题:compaction新生成的文件的热度怎么计算,直接按照t=0计算?那么此时的访问频率还是0,感觉直接放到slow storage也不太合适吧。
迁移的方式包括:主动迁移和compaction迁移
文章4.3节介绍了compaction时自动迁移(此时热度被平均算,算下来可能fast storage的数据会变cold),flush不迁移。
另一个问题时,处在迁移边界的SSTable,可能会频率迁移,作者定义了一个sstable migration resistance参数(由client调参), 代表不会迁移的sstable个数,即使它们的热度变化了。
Evaluation·
实验对照组:
- AWS EC2 with a local SSD
- fast and slow storage, 用一个local attached SSD和一个remote的磁盘
不同device的性能对比

cost 自适应·
用YCS 的 read latest负载,刚好是设定目标cost为0.4 $/GB/month, 之后改为0.2$/GB/mont, 最后改为0.3. 设定热度计算间隔为1s,衰减因子为0.999.
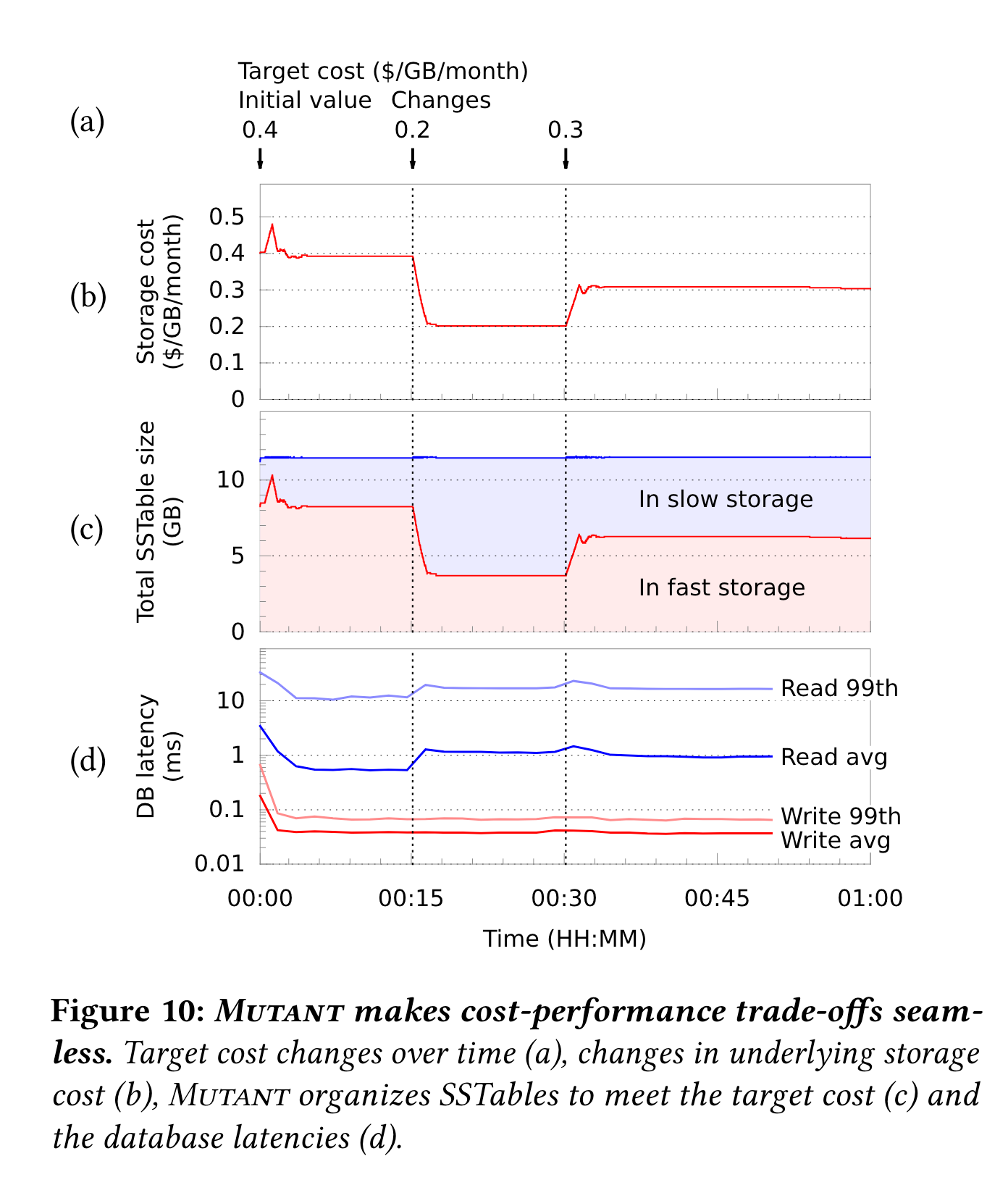
笔者注:数据量太小了。另外图d看不出对照组端到端的时延,只看cold和hot没意义。
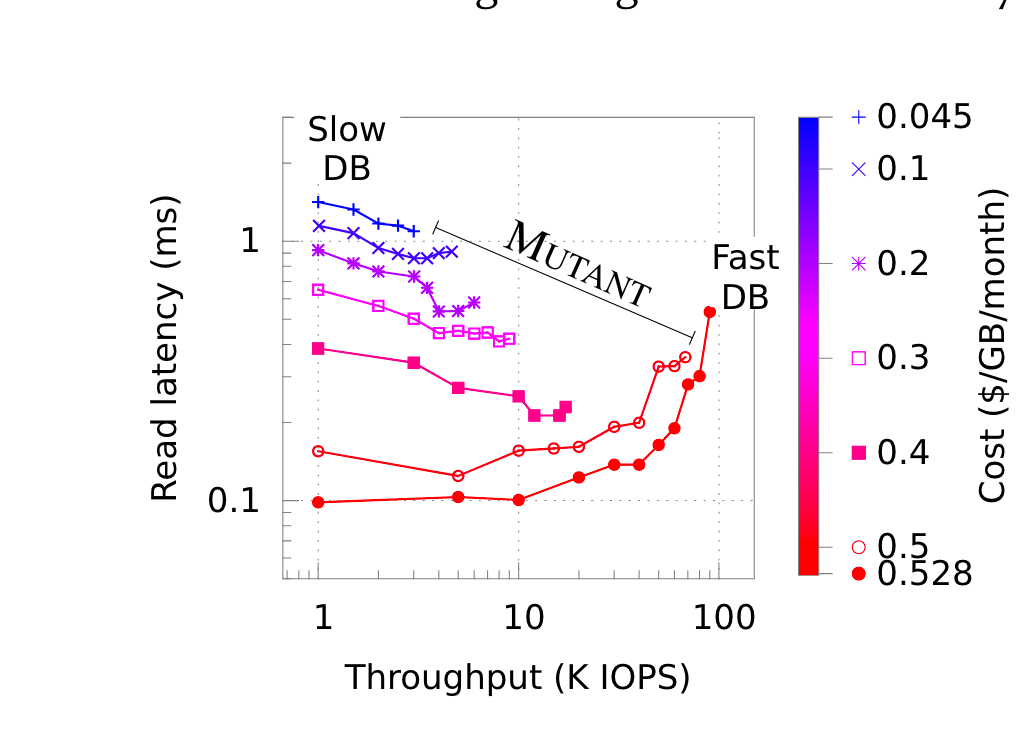
下图展示性价比的频谱:随着cost的增加,latency和吞吐的变化。
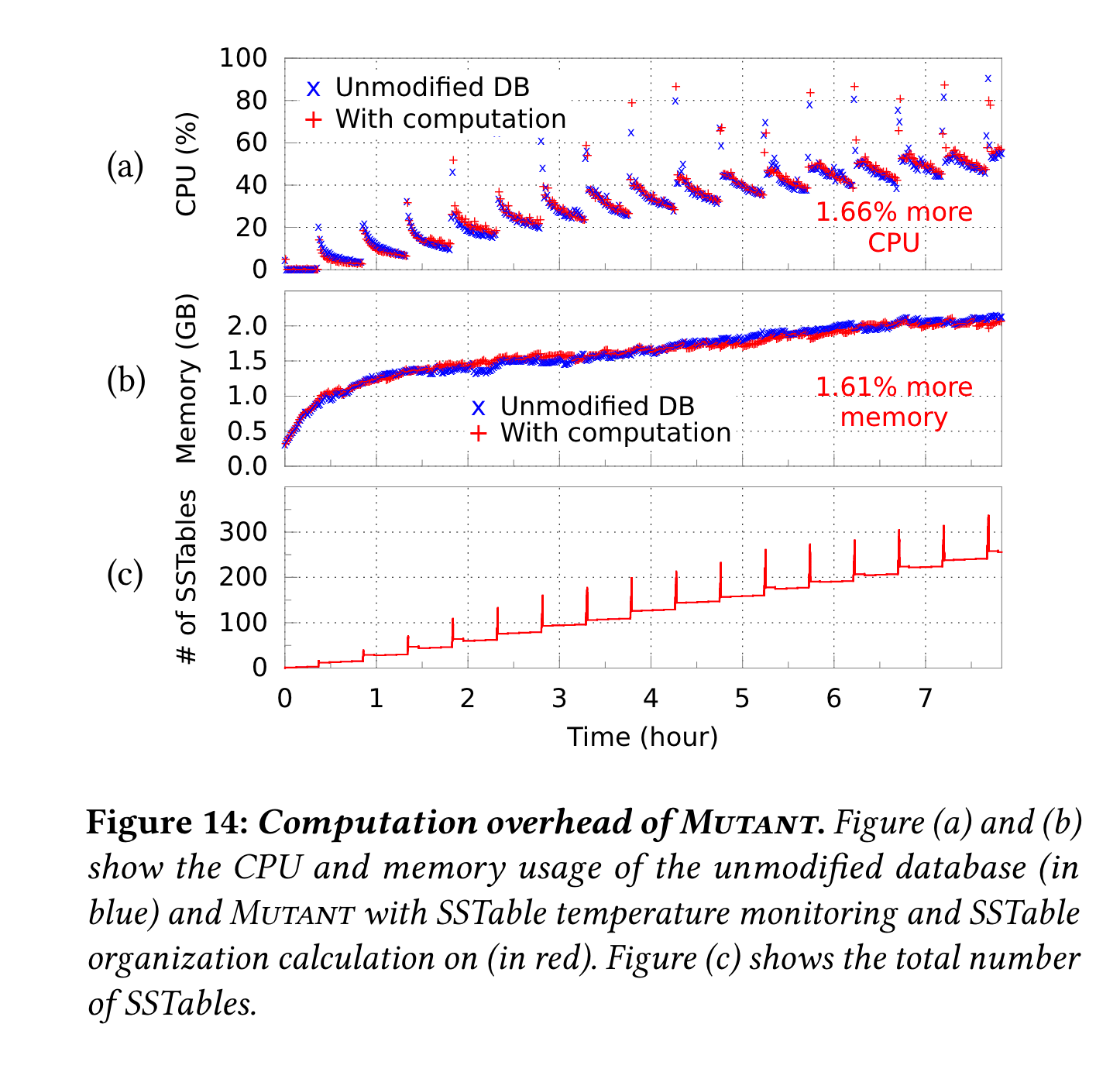
开销对比,对比和原生未修改版本的cpu和mem开销:
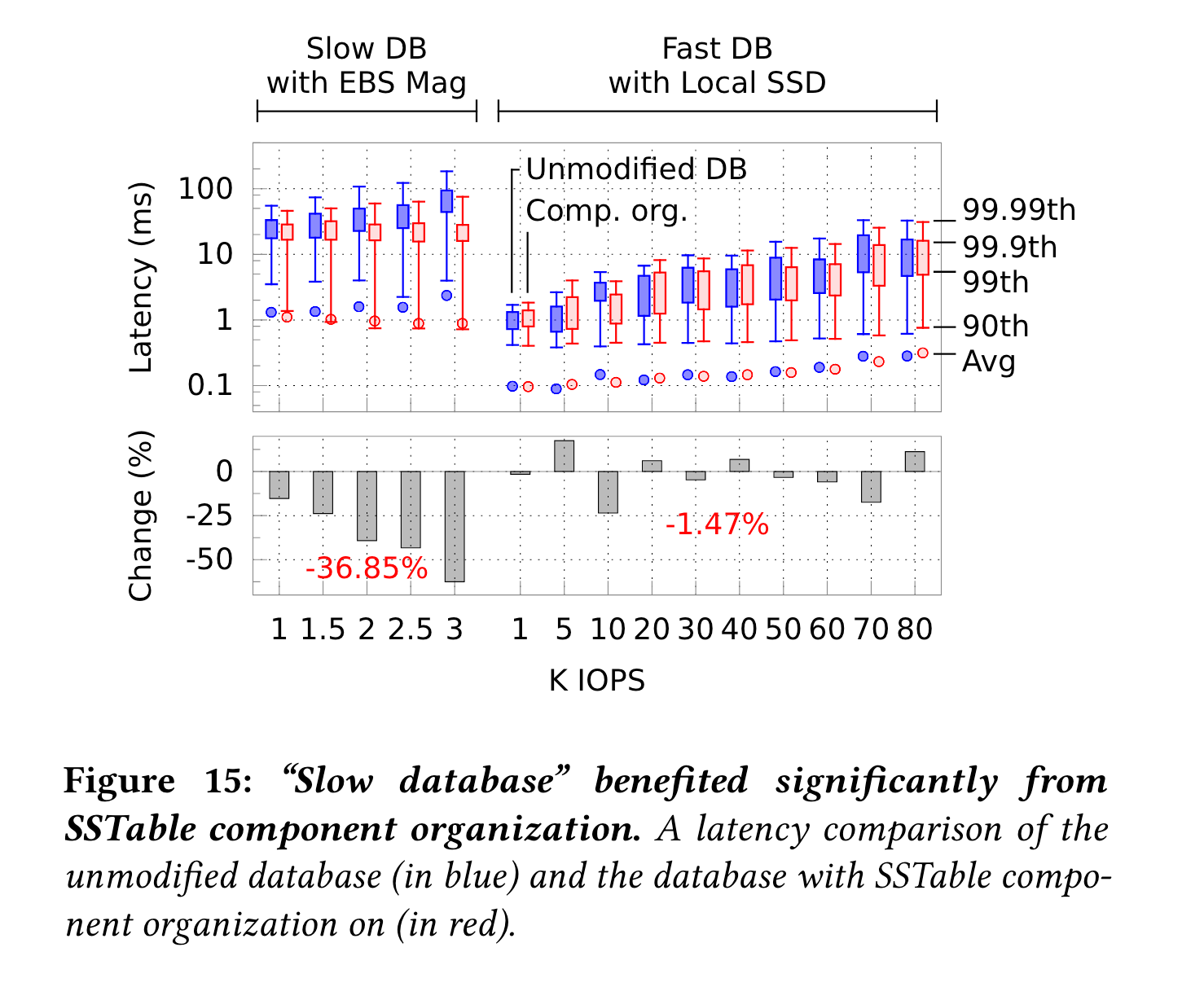
sstable metadata缓存的benefit: slow device受益明显,fast device变化不大。
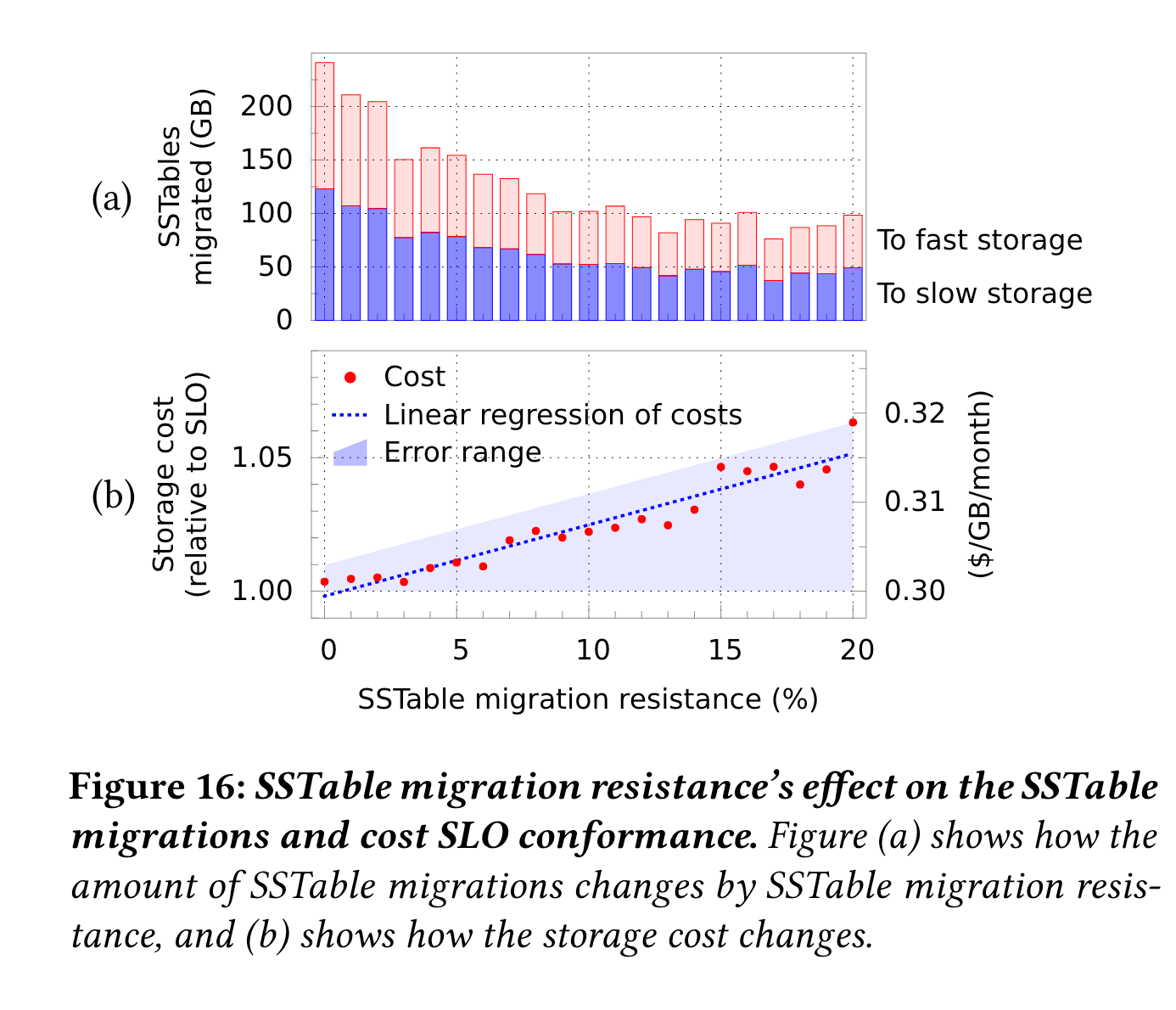
sstable迁移resistance因子影响:因子越大,迁移树越小,但是cost越高。
compaction migration评估:
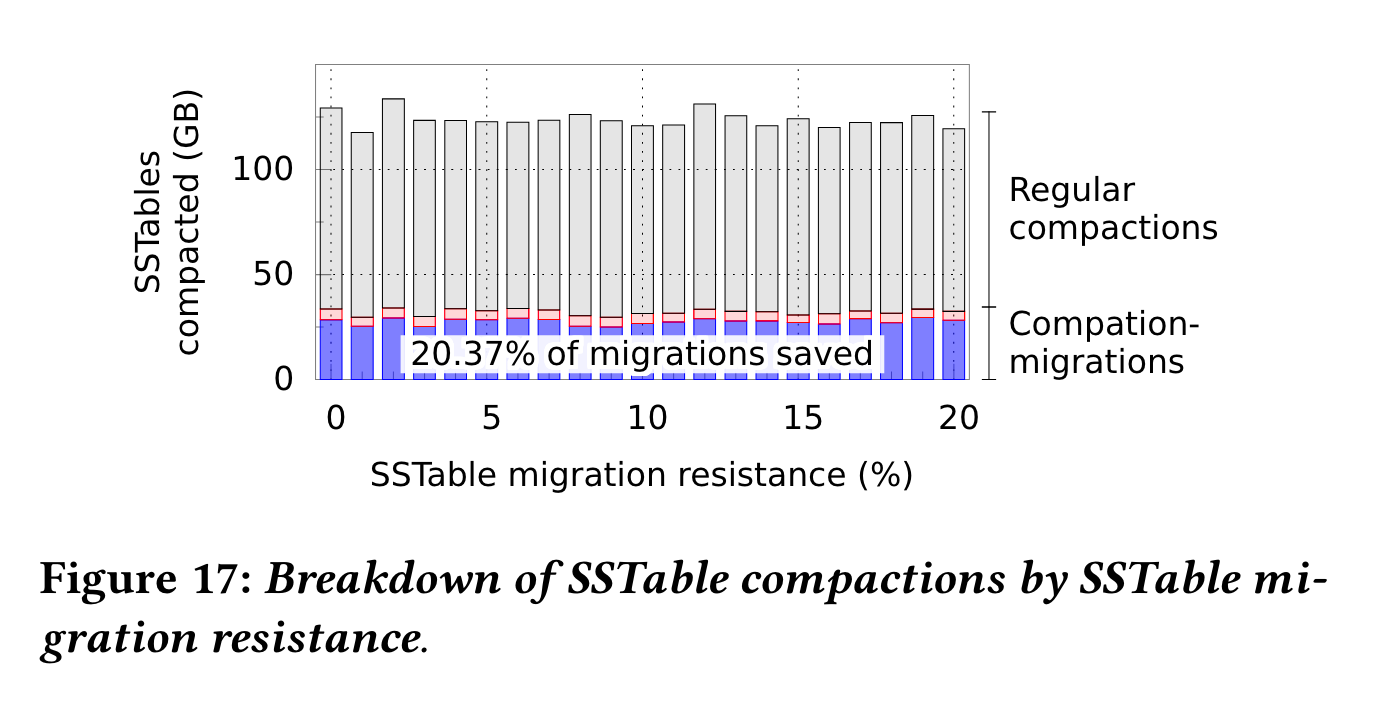
大概有20%的compaction直接转为了migrate,避免double write。
总结·
文章的总体方法非常简单(某种程度上,让我认为是本科生的毕设,某些图表看似好看,但是含义不太清晰,至少我直接看图没法立马明白)。但是数学建模的方法还是值得学习的,怎么简化问题,实验上数据量不够大,云产商至少要有TB级别的数据量。