CMU-15445-proj2-checkpoint1(B+ tree index)

0. 前言·

从这个proj开始，难度上升了很多个档次，做起来明显吃力。

proj2要求实现一个线程安全的B+ tree。收货满满。

1. 要求·

proj2的checkpoint1要求实现B+ tree的节点class，包括internal page和leaf page，以及它们的公共父类parent page。之后在此基础上实现B+ tree的insert和point search。

点这里查看详细要求。

2. 题解·

虽然我之前说过所有projects都不会透漏代码，但是结合我的做题体验来说，我是参考了不少博文和代码才做出来的。所以本文除了记录坑点外，也会贴部分关键的代码或伪代码。对于才开始做的朋友来说，checkpoint1肯定是无从下手的，因为他只是提供了一些函数和注释，不明白具体该做什么。比如下面这个函数：

如果没有做完整个proj，起手就写它的话，我是不知道如何下手的。建议阅读下整个public的函数作用，leaf page同理，然后从b_plus_tree.h/cpp入手。

ok， 建议说完，额外推荐一些学习资料，主要是B+树相关：

1. geeksforgeeks上的B+树文章：这里, 只是介绍了B+树的概念和插入操作代码。
2. B+树删除操作视频：这里
3. B+树删除操作文章：这里
4. B+树开源源码：这里
5. cmu15445课程参考书籍：database system concepts

额外推荐知乎文章中提到的群，我在里面受到了不少帮助，群主在piazza上开设的讨论帖也能找到不少帮助资料。

这里

2.1 B+ tree parent page·

这个类实现起来很方便，要说明的只有两点：

1. size_这个成员变量说的是一个节点的孩子指针个数，而不是key的个数。
2. GetMinSize函数，获取一个节点中最少的孩子指针个数是多少 。

这个给个总结表：

根据书籍p665(DataBase System Concepts第7版)所说，如果规定阶数（也就是一个节点的最大指针分支数量）为n，则
+--------+--------------------------+--------------+------------------------+
|  type  |          最多key         | 最多pointers |      最少pointers      |
+--------+--------------------------+--------------+------------------------+
|  叶子  |            n-1           |       n      |    (n-1)/2 向上取整    |
+--------+--------------------------+--------------+------------------------+
| 非叶子 |            n-1           |       n      |      n/2 向上取整      |
+--------+--------------------------+--------------+------------------------+
|  root  |    n-1(非叶子)或n（叶子）） |       n      |  1（叶子）或2（非叶子） |
+--------+--------------------------+--------------+------------------------+
root节点是特殊的，首先root不用满足节点数量低于一半时分裂，其次
root节点可能是叶子节点，也可能是非叶子节点。如果root节点作为叶子节点，
则key和value的数量一样，此时min size = 1；如果root节点作为非叶子节点，
则key数量=value数量-1，此时min size = 2；

所以GetMinSize的实现为：

int BPlusTreePage::GetMinSize() const {
  if (IsRootPage()) { /* root 节点特殊，需要单独考虑 */
    return IsLeafPage() ? 1 : 2;
  }
  return (IsLeafPage() ? max_size_ : (max_size_ + 1)) / 2;
}

// 额外附上IsRootPage的实现
bool BPlusTreePage::IsRootPage() const { return this->parent_page_id_ == INVALID_PAGE_ID; }

2.2 B+ tree internal Page·

internal page作用为route，value的个数=max_size, key的个数=max_size - 1。 所以key的索引应该从1号位置开始。主要说一下我认为在Checkpoint1中需要实现的重点函数：

1. ValueIndex表示在array数组中找到 array[i].second == 传入的value的 i， 由于value不是有序的，所以目前只能线性扫描

2. Lookup 表示在array数组中找到最大的一个K，这个K满足足K<=key，然后返回这个K的对应V。 采用 二分查找即可。

3. PopulateNewRoot表示this指针所代表的的节点为root节点，且目前size=0, 这个函数要做的工作是设置root节点的左孩子和右孩子分别为old_value和new_value

4. InsertNodeAfter这个没什么好说的，在old_value后面插入new_key和new_value

5. MoveHalfTo, 这个函数将在后续实现B+ tree的插入分裂时使用，初看这个函数不知道如何移动，是移动this node的前半段数据，还是移动this node的后半段数据？ 所以当时我是参考了别人代码，最后知道了是将this node的后半段数据移动到recipient中。参考代码如下：

   /*
    * Remove half of key & value pairs from this page to "recipient" page
    */
   INDEX_TEMPLATE_ARGUMENTS
   void B_PLUS_TREE_INTERNAL_PAGE_TYPE::MoveHalfTo(BPlusTreeInternalPage *recipient,
                                                   BufferPoolManager *buffer_pool_manager) {
     /*
         拆分后，将this->page中节点的一半移动到recipient中
         +----------+    +------------+
         |this page  --->   recipient |
         +----------+    +------------+
     */
   
     int size = GetSize();
     int remain_size = size / 2;
     recipient->CopyNFrom(array + remain_size, size - remain_size, buffer_pool_manager);
     SetSize(remain_size);
   }

6. CopyXXXFrom相关函数，这几个函数主要从拷贝一份数据到this node。 只不过要注意的是，拷贝key value的同时，还需要更改value所代表的的节点的parent_page_id为this->page_id。 如CopyLastFrom函数的参考代码实现：

   /* Append an entry at the end.
    * Since it is an internal page, the moved entry(page)'s parent needs to be updated.
    * So I need to 'adopt' it by changing its parent page id, which needs to be persisted with BufferPoolManger
    */
   INDEX_TEMPLATE_ARGUMENTS
   void B_PLUS_TREE_INTERNAL_PAGE_TYPE::CopyLastFrom(const MappingType &pair, BufferPoolManager *buffer_pool_manager) {
     PushBack(pair.first, pair.second);	// 这个函数是自己添加的
     SetParentToMe(pair.second, buffer_pool_manager);	// 将pair.second所代表的节点的parent_page_id设置为this->page_id
   }
   
   INDEX_TEMPLATE_ARGUMENTS
   void B_PLUS_TREE_INTERNAL_PAGE_TYPE::SetParentToMe(page_id_t page_id, BufferPoolManager *buffer_pool_manager) {
     Page *page = buffer_pool_manager->FetchPage(page_id);
     // 注意对一个page的访问，需要通过buffer_pool_manager来管理
     BPlusTreePage *bp_tree_page = reinterpret_cast<BPlusTreePage *>(page);		
     bp_tree_page->SetParentPageId(this->GetPageId());
     // 访问完成后，还需要unpin
     buffer_pool_manager->UnpinPage(page_id, true);	
   }

ok，重点函数就这些。

2.3 B+ tree leaf page·

leaf page是用于真实存储数据的。key和value的个数都=max_size，所以leaf page的key扫描从索引号0开始。其余函数和internal page类似。

2.4 B+ tree point search·

B+ tree的点查询还是相对简单的，贴一下书中提到的伪代码：

为了实现Search（GetValue)，需要实现FindLeafPage, 实现 FindLeafPage 函数后，GetValue函数就非常简单了。

这里贴一个实现:

/*
 * Return the only value that associated with input key
 * This method is used for point query
 * @return : true means key exists
 */
INDEX_TEMPLATE_ARGUMENTS
bool BPLUSTREE_TYPE::GetValue(const KeyType &key, std::vector<ValueType> *result, Transaction *transaction) {
  if (IsEmpty()) {
    return false;
  }
  /* find leaf page */
  LeafPage *leaf_page = reinterpret_cast<LeafPage *>(FindLeafPage(key));
  ValueType value;
  bool ret = leaf_page->Lookup(key, &value, comparator_);
  if (ret) {
    result->push_back(value);
  }
  /* release */
  buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), false);
  return ret;
}

最后就是checkpoint1的重头戏，实现insert函数，因为insert涉及到分裂，所以要实现以下函数：

1. StartNewTree如果当前tree还是空的，则调用本函数，生成root节点。
2. InsertIntoLeaf，如果当前tree非空，则将key,value插入到叶节点。

贴一个伪代码：

具体实现时，无需将整个旧节点都拷贝一份，然后再一半一半的分别拷贝到两个孩子节点。只用将原本满的节点当作左孩子，然后申请一个右孩子即可。

然后是两个子函数：

额外关注，proj中的B+ tree是不支持重复key插入的，所以在真正执行插入前，可以Lookup一次key是否已经存在叶节点中，如果已经存在则直接return。

这里贴一下InsertIntoLeaf中的核心代码：

LeafPage *left_page = leaf_page;
LeafPage *right_page = Split<LeafPage>(left_page);
right_page->SetNextPageId(left_page->GetNextPageId());
left_page->SetNextPageId(right_page->GetPageId());

/* Insert to parent */
KeyType key2parent = right_page->FirstKey();
InsertIntoParent(left_page, key2parent, right_page);

/* unpin pages */
buffer_pool_manager_->UnpinPage(left_page->GetPageId(), true);
buffer_pool_manager_->UnpinPage(right_page->GetPageId(), true);

先分裂，然后取右孩子的第一个key，插入到parent节点中。

Split函数：

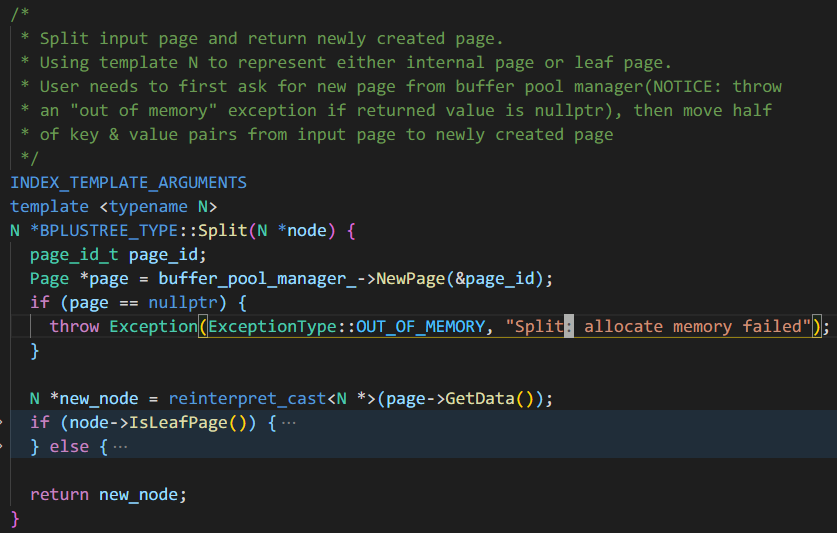
Split时，叶节点和内部节点需要单独处理。

最后是InsertIntoParent， InsertIntoParent是一个递归函数。关键点：

1. 如果old_node已经是root page，那么直接生成新的root page，并设置old_node, new_node的parent_page_id
2. 如果old_node不是root page, 需要找到parent_page, 执行插入，然后检查parent_page是否已满，如果满递归分裂插入。

其中第2点中所说的是否已满的判断条件为：

if (parent_page->GetSize() == parent_page->GetMaxSize() + 1) {
  InternalPage *left_page = parent_page;
  InternalPage *right_page = Split<InternalPage>(left_page);
  /* 提升右节点的第一个key */
  KeyType key2parent = right_page->KeyAt(0);
  // right_page->Remove(1);
  InsertIntoParent(left_page, key2parent, right_page);
  xxx
}

为什么是 max_size + 1?

首先这里的parent_page肯定内部节点。现在考虑如下的场景：如果tree初始化的leaf_max_size=2, internal_max_size=3。 之后依次插入1,2,3。 插入2时，[1,2]这个节点将分裂一次，得到root节点[2], 叶节点[1]和[2]。 然后插入3， 此时[2,3]这个节点会分裂一次，叶节点为[1],[2],[3]。 同时内部节点为[2,3], 此时内部节点因为达到了max_size=3(因为三个孩子），所以再次触发分裂，不过此时是没办法分裂的。结果如下图：

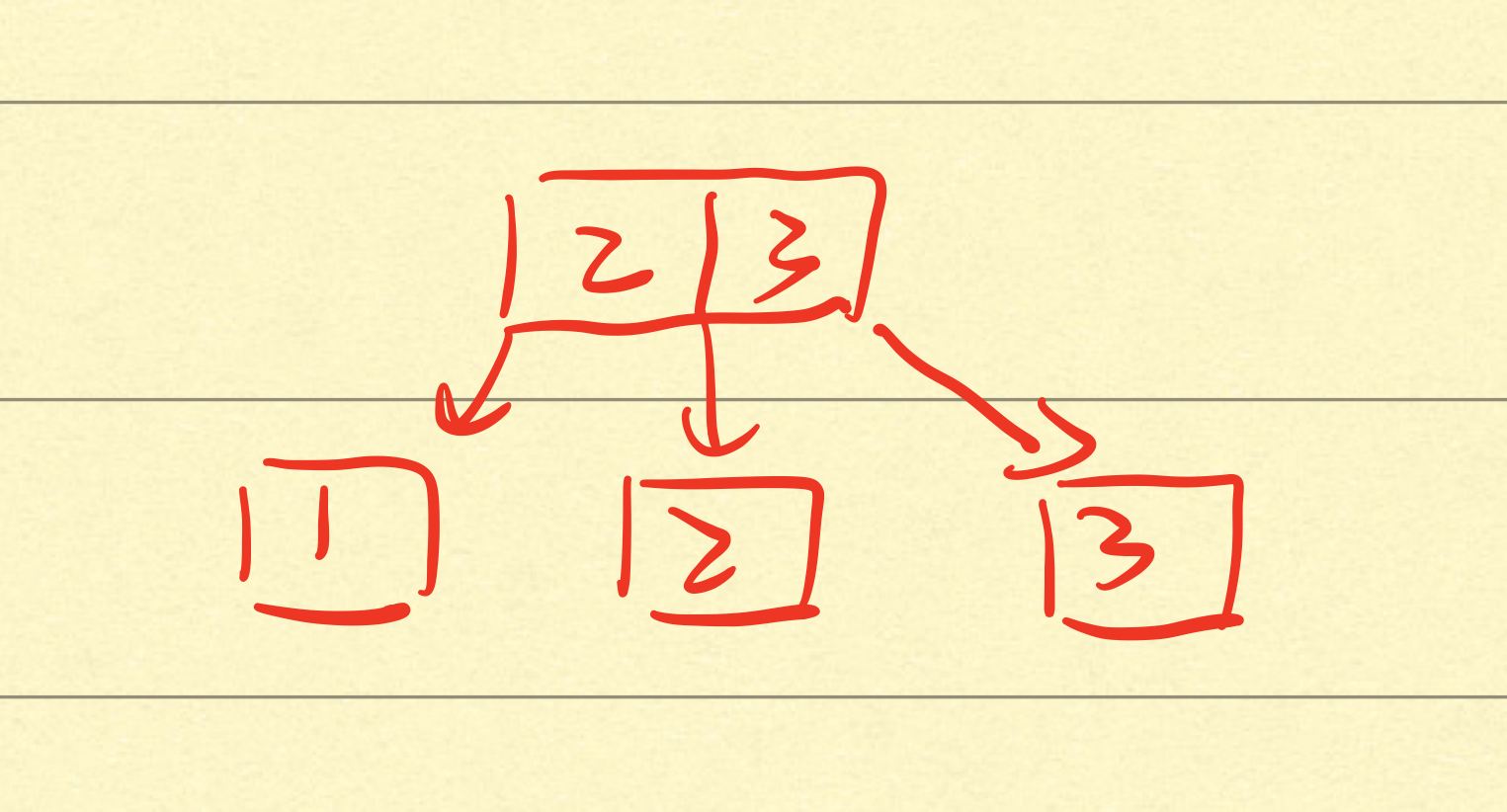
[2,3]这个节点是不可能分裂出去的。

此时你可能要问，强制要求internal_max_size 不能小于3，即必须>=4不就可以了吗。这个不行，因为官方提供的测试用例中，有一句：

所以，实现中必须兼容internal_max_size=3的情况。

那内部节点的分裂时机设置为size == max_size + 1有什么问题？ 有问题，那就是可能产生越界的情景。默认为的INTERNAL_PAGE_SIZE为：

#define INTERNAL_PAGE_SIZE ((PAGE_SIZE - INTERNAL_PAGE_HEADER_SIZE) / (sizeof(MappingType)))

所以当插入第max_size + 1个元素时，实际上是插入到下一个page去了。

那该怎么处理？两种方案：

1. 先检查是否可能造成分离，如果会，则先分裂，再插入。这种方案可行，但是实现麻烦。
2. 修改INTERNAL_PAGE_SIZE的默认值，留一个空槽出来即可。

这里采用方案2，修改下宏定义即可：

#define INTERNAL_PAGE_SIZE (((PAGE_SIZE - INTERNAL_PAGE_HEADER_SIZE) / (sizeof(MappingType))) - 1)

3. 其它坑·

如果一切梳理，至此你可以通过本地print test，通过dot file和graphviz绘制出自己的B+ tree。 但是可能提交到 gradescope 上只能得到20分。 在memory_test上会丢失10分。

原因大概率是是因为 buffer_pool_manger这个类有点问题，即使顺利通过了proj1，也是有可能有问题。常见问题有两个：

1. UnpinPageImpl实现中，对于 page_table找不到的 page_id ，需要返回true
2. DeletePageImpl实现中，处理 擦除page_table中的元素，归还到free_list中以外，还需要从 replacer_中踢出相应的 frame_id

ok，大概就是这么多。